Quicklinks
| Download Program: | wedo-speed-governor.WeDo |
| This Page as PDF: | wedo-speed-governor.pdf |
| Video: | Youtube Video |
Lego WeDo Speed Governor
The centrifugal speed governor is a mechanical device to measure and control the speed of a machine by transforming the rotational speed to a mechanical displacement. A model is built and programmed using Lego WeDo to demonstrate the physics behind it.
Video
Description
Two weights (yellow-red Lego blocks) are attached to a rotating axle like a pendulum. The faster the axle spins the bigger the angles between the axle and the attached weights become. Through a mechanism, this angles are transformed to a vertical displacement of the white platform. The faster the rotation, the bigger the angle and the lower the position of the platform.
The platform could now be connected to a controlling device, like a valve. Systems like this were used since the 18th century as a mechanical “cruise control” for steam engines with the valve controlling the steam flow to the engine.
The WeDo program

The WeDo program used for the speed governor starts when the “A”-key is pressed. First, the number 10 is stored in the display and the motor set in motion at full speed (10).
Jetzt startet eine 10-Fache Schlaufe. Bei jedem Durchlauf wird, nach einer Wartezeit von 100, eins vom Wert der Bildschirmvariablen abgezogen und diese als neue Motorgeschwindigkeit festgelegt. Dadurch wird der Motor bei jedem Durchgang etwas langsamer, bis er schliesslich ganz stehen bleibt.
The physics of the centrifugal speed governor
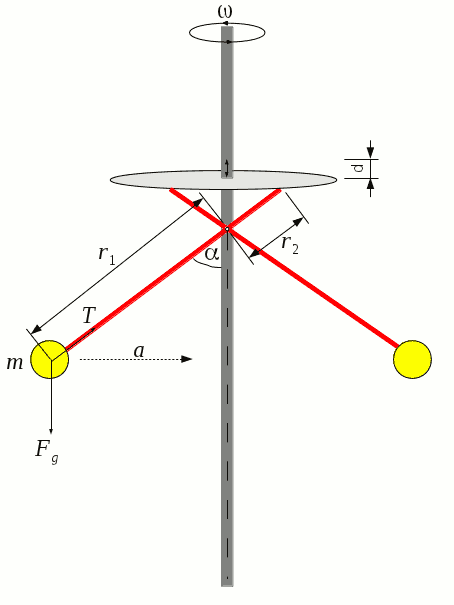
From Newtons second law we get in vertical direction
T⋅cos(α)-m⋅g=0 → T=m⋅g/cos(α)
and horizontally:
T⋅sin(α)=m⋅a → tan(α)=a/g
The centripetal (center seeking) acceleration a of a uniform circular motion is:
a=r⋅ω2 → a=r1⋅sin(α)⋅ω2
Combining the equations 2 and 3 we get:
cos(α)=g/(r1⋅ω2)
And finally for the horizontal displacement d:
d=r2⋅cos(α) → d=r2⋅g/(r1⋅ω2)
As d can only be between 0 and r2, there is a interesting limitation for equation 5:
ω≥√(g/r1)
That limitation actually was present in equation 4: cos(α) only exists between 0 and 1. Which is the case if ω≥√(g/r1)
The physical meaning of the working range limits of the centrifugal speed governor
The centrifugal force required to keep the weights of the governor at an angle α is: Freq=tan(α)⋅g⋅m
However the centrifugal force produced by the rotation is F=sin(α)⋅r1⋅ω2⋅m
For ω smaller than specified by equation 6. The produced centrifugal force is not high enough to balance out the gravity. The arms of the governor will therefore not be lifted.
Building Guide
 |
Needed Material On the left you see the material that is needed to build the speed governor. All the items can be found in the WeDo package. |
The Speed governor
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
|